디아블로 이모탈을 본 단상

Diary|2018. 11. 8. 20:44

디아블로 이모탈(Diablo immortal) 을 본 단상


2018년 11월 3일.

온라인 세상은 블리즈컨의 열기로 가득했다.[각주:1] 이전부터 새로운 무언가를 보여준다며, 팬들의 기대를 가득 불러일으킨 디아블로의 발표 시간이 첫날과 마지막에 잡혀있었던 것이다. 


첫날과 마지막날 이면, 당연히 중요한 발표일거야.


멍청한 생각이었다. 하지만, 이 시점 까지는 아무도 모르고 있었기에, 나도 새벽같이 일어나 발표를 보기 위해 자리를 잡았다.

사실은, 침대에 누운 그대로 핸드폰만 들었다.


짖궂은 사람들은, "너의 디아블로 모바일로 대체되었다[각주:2]" 라며 GIF까지 만들어대고 있었다.




말도 안되는 얘기였다.

아니, 말도 안되는 얘기여야만 했다.


그리고, 대망의 발표.


와이엇 쳉분의 등장과 함께 장내는 환호로 가득찼다. 스마트폰의 유리 화면 뒤 나의 마음속도 환호로 가득찼다. 비록 방음이 못미더운 자취방 한 구석이라 소리는 못냈지만.


그리고 그는 말했다.


"새로운 디아블로"


환호를 지르려는 순간, 부족한 내 영어 청음으로도 듣고 말았다. "모바일"


환호가 야유로 바뀌는건 순식간 이었다.

그리고 나는, 내 자취방의 방음 성능을 확인하고 말았다.


"X발"


아마 믿어도 좋은 방음 이리라, 아직 자취방 주인 아주머니의 퇴거명령이나, 문 앞에 조용히 해달라는 쪽지가 생기지 않은걸로 보아선 말이다.


"X씨X"


사실 두번 소리질렀다.

아니 사실 셀수 없이. 그래도 소리 지른건 단 두번이고, 나머지는 혼자 씹어뱉은 욕지거리였으니, 이 글을 보는 독자분들은 나를 용서해주길 바란다.

나는 최대한 노력했다.


그래도 애써 마음을 다잡았다.


"그래. 그래도 블리자드 잖아. 하스스톤도 모바일로 나왔다고? 어떤 새로운 경험을 줄지 몰라"



이건 상상도 못했었다.

블리자드 게임 발표 트레일러에서 외주 제작사 로고라니? 그것도 중국 양산형 모바일 게임을 만드는 회사라니?


넷이즈라는 이름이 생소하시다면, 혹시 올해 논란이 되었던 DIA M 을 기억하시는가?

디아블로와 유사하게 생긴 양산형 모바일 RPG. 그 회사가 넷이즈다.



회장은 야유로 가득찼다.

무대에 토마토가 날아들지 않는것을 보며, 선진국 국민들의 높은 시민의식에 감탄을 하기도 잠시, 미려한 트레일러는 오히려 마음을 심란하게 하였다.

이게, PC RPG 였더라면...


그리고 트레일러에 공개된 UI는 새로운 조작법이나 무언가를 보여주지 않을까 했던 내 마지막 기대마저 찬찬히 부수어 갔다.

차라리 잠이나 더 잘껄.


그리고 이후 QnA 세션.

여기서 전설로 남은 그 질의가 나온다.


Q: PC나 다른 콘솔로는 안나오나요?

A: 네, 어쩌구 저쩌구... 여러분은 스마트폰도 없나요?


오... 하나님.



  1. 블리즈컨 : 블리자드에서 매년 여는 행사로, 새로운 게임/확장팩 등을 공개하는 행사 [본문으로]
  2. 인터넷에서 유행하는 번역체 드립. 너의 OOO OOO로 대체되었다. [본문으로]
저작자표시 비영리 변경금지

'Diary' 카테고리의 다른 글

오버워치 PPT 템플릿 블로그가 되어버렸다.  (0) 2018.11.16

댓글()

VGG Net

Study-Machine Learning/Deep Learning|2018. 11. 8. 20:18

VGG Net

Very Deep Convolutional Networks for Large-Scale Image Recognition SIMONYAN, Karen; ZISSERMAN, Andrew. 1

1. 서론

VGG Net은 2014년 ImageNet 대회에서 Classification 에서 2위, Localization에서 1위를 한 모델이다. Classification 1위는 Google의 GoogLeNet2 으로, 이 모델에서 나온 Inception 모델은 아직도 많이 논의되고있다. VGGNet은 GoogLeNet 보다 비록 성능은 뒤졌지만, 훨신 간단하고, 따라서 각 Epoch가 빠르며, 이해와 변형에 용이하여 현재도 많은 연구에서 차용하고 있다.

이 모델의 이 논문 이전의 논문들과 다른, 가장 큰 특징은 두가지 이다.

  • 첫번째는 3x3의 작은 filter만을 사용한 CNN모델 이라는 점 이다.
  • 두번째는 16/19 레이어의 깊은 레이어를 사용한다는 점 이다.
    (현재 일반적으로 두 모델을 각 VGG16/VGG19로 부른다.)

2. 특징

VGGNet을 설명한 논문인 Very Deep Convolutional Networks for Large-Scale Image Recognition1 은 모델의 깊이의 영향을 분석하고자 했다. 이를 위해 3x3의 매우 작은 Filter를 가지는 Conv레이어를 여러 층 쌓아 깊게 만들어서, 깊이의 영향력을 보였다.

레이어의 깊이와 오류율 변화 추세
레이어의 깊이와 오류율 변화 추세3

위의 그림에서 보이듯, VGG Net 전까지는 최대 8레이어의 비교적 얕은 모델이 주류를 이뤘으나, VGG Net 이후 깊은 레이어가 잦게 사용되면서, 다음년도 1위를 차지한 ResNet3 의 경우에는 152 레이어를 사용하였다.

이렇듯 깊은 레이어를 사용하는것은 결정 함수의 결정력을 키워주는 효과가 있다. (본문 : makes the decision function more discriminative.) 하지만, Layer의 수가 늘어나면 (망이 더 깊어(Deep)지면) 문제가 생긴다. 우선, 망이 깊어질수록 Paremeter의 수가 증가하며, 이는 연산속도의 저하와, Overfitting 의 위험을 키우는 효과가 있다.

이를 위해, VGG Net 에서는 각 필터의 크기를 3x3으로 작은 필터를 사용하였다. 이 논문 이전, 기존의 State Of the Art 였던 7x7 필터 하나 대신, 3x3 필터 3개를 사용하였을 경우, 레이어의 수를 C 로 하였을 때, 파라미터의 수는 아래와 같다.

  • 3x3 필터 3 레이어의 경우 : 3(32C2) = 27C2
  • 7x7 필터 1 레이어의 경우 : 72C2 = 49C2

본 논문에서는 깊이에 따른 성능 변화를 비교하기 위해 다양한 모델을 구성하였다.
A부터 E 까지 각각, A를 기본으로, LRN(Local Response Normalization: 정규화의 일종) 을 추가한 모델 A에 레이어를 추가시킨 B, B에 레이어를 추가시키되, Conv로 인한 영향이 없이 Non-Linearity만을 늘이기 위한 방법으로 1x1 Conv를 3개 추가한 C, C의 대조군 으로, 3x3 Conv레이어를 3개 추가한 D(VGG 16) 그리고 D에 3x3 Conv 레이어를 3개 추가한 E(VGG 19)로 구성했다.

네트워크 구성 A-E
네트워크 구성 A-E1

1x1 Conv 레이어는 특이한 발상인데, 이는 Convolutional의 영향은 줄이면서 Non-linear 의 영향은 발휘하는 레이어 이다. 이 논문에서는 같은 사이즈의 Input/Output 을 적용하여, 단지 위의 이유만으로 사용했지만 Network in Network4(이하 NIN) 라는 논문에서는 Mlpconv (NIN에서 제안하는 모델로, Conv 레이어의 결과를 그대로 Conv에 넘기는 기존 방식에서, FC레이어를 뒤에 붙여 Non-linearity를 높힌 모델, Global Average Pooling도 NIN에서 처음 제안되었다.)에도 이를 적용하여 사용하였다.

3. 결과

결과
결과1

각 레이어별로 실험한 결과 위와 같은 결과가 나왔다.

A와 A-LRN 을 비교한 경우 큰 차이가 없으므로, CNN모델에서 중간에 들어가는 정규화는 큰 의미가 없음을 확인 가능하다. B와 C를 비교했을 때, 큰 차이가 없으므로, 깊은 학습은 Convolutional을 통한 분할이 중요함을 확인 가능하다. 여기서 주목할 만한 사항은, D와 E를 비교했을 때, 깊을수록 더 좋은 결과를 보이던 이전까지와 달리 같거나 나쁜 성능을 보이고 있는 점 이다. 이는, Vanishing-gradient로 해석 가능하다. 하지만, 이 논문의 경우 Activation-function 으로 ReLU를 사용하였는데도 위와 같은 현상이 발생하였다. 따라서 저자들은 E 이후로 더이상 레이어를 늘리기를 멈추었다. 이를 해결하여 레이어를 152개까지 쌓은 논문이 ResNet으로, ResNet은 일정 갯수의 레이어 마다, 몇 단계 이전의 레이어의 결과를 앞으로 가져오는 정책을 통해, 해당 이슈를 해결하였다. (이외에도, DenseNet 등이 해당 이슈를 각자의 방식으로 해결하여 논문을 출판)

4. 학습 방식

이 논문에서, VGG Net은 독특한 학습 방식을 가진다. 이전보다 깊어진 네트워크를 효율적으로 학습시키기 위해, A부터 E 까지 A를 학습 시키고, 여기에 레이어를 추가 시켜서 B를 추가 학습 시키는 방식으로 학습을 진행하였다. -Bootstrapping?-

enter image description here

또한, 이미지의 갯수를 늘이기 위해, 244*244 보다 큰 크기의 이미지의 경우 다양한 방식으로 이미지를 잘라내어 사용하였다. 이 부분의 경우 자세히 다루지 않고 넘어가도록 하겠다.

  1. SIMONYAN, Karen; ZISSERMAN, Andrew. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014. ↩︎ ↩︎ ↩︎ ↩︎

  2. SZEGEDY, Christian, et al. Going deeper with convolutions. In: Proceedings of the IEEE conference on computer vision and pattern recognition. 2015. p. 1-9. ↩︎

  3. HE, Kaiming, et al. Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition. 2016. p. 770-778. ↩︎ ↩︎

  4. LIN, Min; CHEN, Qiang; YAN, Shuicheng. Network in network. arXiv preprint arXiv:1312.4400, 2013. ↩︎


저작자표시 비영리 변경금지

'Study-Machine Learning > Deep Learning' 카테고리의 다른 글

CAM - Class Acvtivation Map 논문 (Learning deep features for discriminative localization) 리뷰  (0) 2018.11.15
VGG Net 과 CAM (Class Activation Map) 구현  (0) 2018.11.14
4. CNN : Convolution Neural Nerwork with keras  (0) 2018.07.21
3.DNN : DeepNeauralNetwork with keras  (0) 2018.07.19
2.simple ANN with Keras  (0) 2018.07.18

댓글()

연구실 에서 살아남기 -5- 대학원에 적합한 사람

Diary/연구실 에서 살아남기 |2018. 10. 16. 11:41

서론

 연구에 적합한 사람이란 누구일까? 혹자는 영화나 미디어에서 보이는 소위 "천재 과학자"를 떠올릴지도 모르겠다. 하지만 내가 겪은 대학원은 "천재 과학자"는 "천재" 니까 살아남을수 있는 세계이다.


본론

 

대학원 입학 전에 당신의 머릿속에 있는 연구자/과학자란 어떤 이미지 인가? 십중 팔구, 어딘가의 매드사이언티스트 일것이다. 그런 미디어에 나오는 이미지에 현혹되지 말라고 해도, 직접 만나보지 못하니 어쩔수 없다는 항변이 나오는 것도 당연지사.


[괴짜 과학자 이미지의 스테레오타입은 이 분부터 시작이 이닐까?]


 왠지 독특하고 남들과 다른 행동을 하는 소위 Geek한 이미지를 떠올리는 그대에게, 가장 가까운 곳에 있는 과학자를 소개해 드리고자 한다. 바로 여러분의 교수님이시다. 우리가 주변에서 가장 쉽게 볼수있는 성공한 과학자는 오늘도 열심히 씹었을 바로 교수님 이시다. 그 분이 Geek 하던가?

 

 물론, Geek한 분이 없다는건 아니지만, 대부분의 교수님은 오히려 신사답고 매우 꼰대스러울 것이다. 그렇다 그게 바로 과학자다.

 

 대학원 생활은 자칫하면 낭비하기 딱 좋은 구조이다. 출퇴근은 랩마다 관리 하기도 하지만, 그 이외의 업무등은 자기 스스로의 관리하에 놓여있다. 그런 삶을 성공적으로 마치기 위해 필요한 것은 오히려 극단적인 자기통제이다. 여러분이 미디어 에서 접한 소위 "천재과학자"는 "천재"니까 그런 괴짜로 박사가 가능한게 아닐까 싶다. 대부분의 대학원생은 자기 통제에 능하며, 규칙적인 삶을 사는 사람들이다. 특히 성공하는 사람일수록.

 

 그럼 필자는 어떻냐고? 필자는 천재가 되기 위해 끊임없는 노력중이라고만 전하겠다.


 본론으로 돌아와서, 대학원을 생각하는 여러분은 자신같이 평범하게 공부만 하던 학생은 대학원에 가면 안된다고 생각할지도 모른다. 엉덩이가 무겁고 학점 잘 따는 당신, 당신이 바로 내일의 대학원 스타! 


[대학원은 당신을 기다립니다.]


 만약, 자신의 독특한 발상과 Geek한 당신이라면, 주변에선 당신을 대학원에 가서 공부를 더 할 인재로 볼지도 모른다. 그렇다면 가까운 교수님과 진지하게 상담해 보시라. 감히 예측하건데, 스타트업 이나 실리콘벨리를 추천하시지 않을까? 물론 당신이 그러면서 학점과 자기관리가 잘 된다면, 당신 혹시 천재 아냐?

 

그럼 즐거운 연구가 되길 바라며(만약 가능하다면...) 이만 도망가도록 하겠다.

 

저작자표시 비영리 변경금지

'Diary > 연구실 에서 살아남기 ' 카테고리의 다른 글

연구실에서 살아남기 -4- 랩 컨택하기  (0) 2018.04.17
연구실에서 살아남기 -3- 논문 작업  (0) 2018.03.21
연구실에서 살아남기 -2- 과제  (1) 2017.05.22
연구실에서 살아남기 -1- 월요일 주간보고  (0) 2017.05.15

댓글()

4. CNN : Convolution Neural Nerwork with keras

Study-Machine Learning/Deep Learning|2018. 7. 21. 00:07


CNN : Convolution Neural Nerwork

import keras
from keras import models, layers
from keras import backend

D:\ProgramData\Anaconda3\envs\tensorflow-gpu\lib\site-packages\h5py\__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.
  from ._conv import register_converters as _register_converters
Using TensorFlow backend.

필기체 인식

class cnn(models.Model):
    def __init__(self, input_shape, num_class):
        relu = layers.Activation('relu')

        inL = layers.Input(shape=input_shape)

        conv0 = relu(layers.Conv2D(32, kernel_size=(3,3))(inL))
        conv1 = layers.Conv2D(64, (3,3), activation='relu')(conv0)
        maxpool = layers.MaxPooling2D(pool_size=(2,2))(conv1)
        drop_and_flat = layers.Flatten()(layers.Dropout(0.25)(maxpool))
        fc0 = relu(layers.Dense(128)(drop_and_flat))
        drop = layers.Dropout(0.5)(fc0)
        out = layers.Activation('softmax')(layers.Dense(num_class)(drop))     

        super().__init__(inL, out)
        self.compile(loss=keras.losses.categorical_crossentropy, optimizer='rmsprop', metrics=['accuracy'])

CNN의 경우 keras에서 바로 제공하는 CNN Layer가 존재하지는 않는다.

하지만, Convolutional layer와 paxpool 그리고 flatten 등 필요한 layer들은 미리 만들어져서 제공된다.

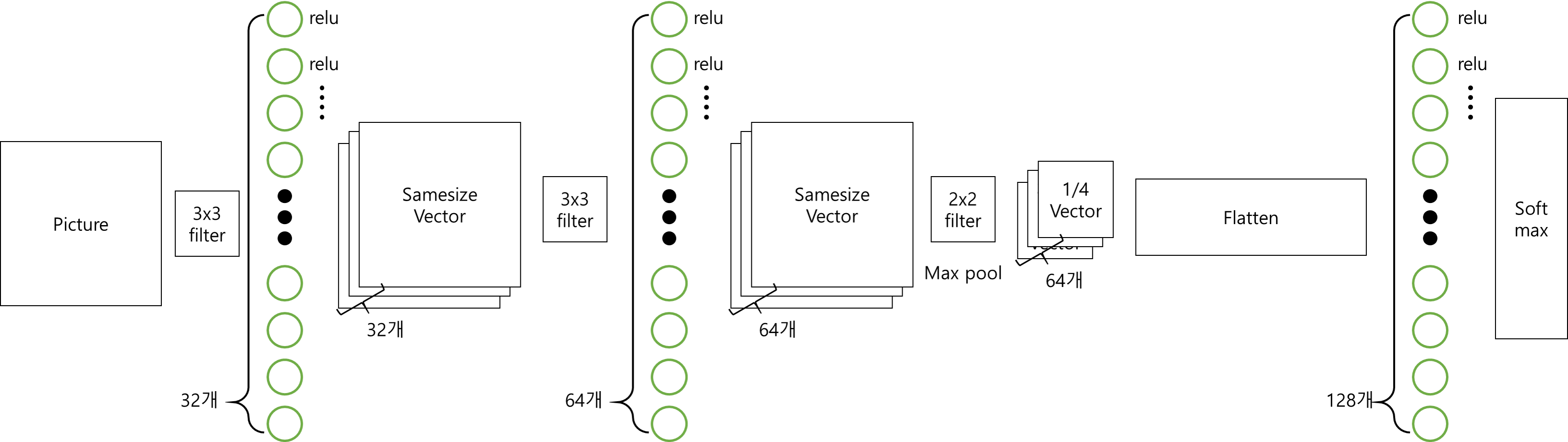
우리가(내가 (사실 참고한 책이) ) 설계한 모델은 아래와 같다

이는 LeNet 모델을 약간 변형한 것 이다.(두번째 Conv 레이어가 32개에서 64개) cnn

from keras import datasets
class DATA():
    def __init__(self):
        num_classes = 10
        (x_train, y_train), (x_test, y_test) = datasets.mnist.load_data()

        self.X_test = x_test
        self.Y_test = y_test

        img_rows, img_cols = x_train.shape[1:]

        if backend.image_data_format() == 'channels_first':
            X_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)
            X_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)
            input_shape = (1, img_rows, img_cols)
        else:
            X_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
            X_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
            input_shape = (img_rows, img_cols, 1)



        X_train = X_train.astype('float32')
        X_test = X_test.astype('float32')

        X_train /= 255.0
        X_test /= 255.0

        Y_train = keras.utils.np_utils.to_categorical(y_train, num_classes)
        Y_test = keras.utils.np_utils.to_categorical(y_test, num_classes)

        self.input_shape = input_shape
        self.num_classes = num_classes
        self.x_train, self.y_train = X_train, Y_train
        self.x_test, self.y_test = X_test, Y_test

데이터를 가져오고, 선처리하는 과정은 여태까지와 같다.

from kerasapp.skeras import plot_acc, plot_loss

import matplotlib.pyplot as plt

batch_size = 128
epochs = 10

data = DATA()

model = cnn(data.input_shape, data.num_classes)

위의 CNN 클래스 에서, 다음과 같이 정의하였다.

self.compile(loss=keras.losses.categorical_crossentropy, optimizer='rmsprop', metrics=['accuracy'])

따라서, optimizer로는 rmsprop를 loss로는 crossentropy를 사용하는것을 알 수 있다.

수행 결과

history = model.fit(data.x_train, data.y_train, batch_size=batch_size, epochs=epochs, validation_split=0.2)

Train on 48000 samples, validate on 12000 samples
Epoch 1/10
48000/48000 [==============================] - 11s 222us/step - loss: 0.2380 - acc: 0.9255 - val_loss: 0.0625 - val_acc: 0.9807
Epoch 2/10
48000/48000 [==============================] - 7s 140us/step - loss: 0.0857 - acc: 0.9747 - val_loss: 0.0498 - val_acc: 0.9864
Epoch 3/10
48000/48000 [==============================] - 7s 137us/step - loss: 0.0657 - acc: 0.9805 - val_loss: 0.0427 - val_acc: 0.9877
Epoch 4/10
48000/48000 [==============================] - 7s 138us/step - loss: 0.0553 - acc: 0.9841 - val_loss: 0.0454 - val_acc: 0.9871
Epoch 5/10
48000/48000 [==============================] - 7s 137us/step - loss: 0.0485 - acc: 0.9859 - val_loss: 0.0415 - val_acc: 0.9890
Epoch 6/10
48000/48000 [==============================] - 7s 137us/step - loss: 0.0430 - acc: 0.9873 - val_loss: 0.0398 - val_acc: 0.9896
Epoch 7/10
48000/48000 [==============================] - 7s 137us/step - loss: 0.0419 - acc: 0.9871 - val_loss: 0.0401 - val_acc: 0.9892
Epoch 8/10
48000/48000 [==============================] - 7s 137us/step - loss: 0.0408 - acc: 0.9881 - val_loss: 0.0464 - val_acc: 0.9887
Epoch 9/10
48000/48000 [==============================] - 7s 137us/step - loss: 0.0424 - acc: 0.9879 - val_loss: 0.0465 - val_acc: 0.9889
Epoch 10/10
48000/48000 [==============================] - 7s 136us/step - loss: 0.0447 - acc: 0.9871 - val_loss: 0.0462 - val_acc: 0.9894

DNN에서보다 훨신 적은 10번의 Epoch를 돌렸다.

Epoch와 Batch의 의미를 알아보자.

Epoch

Epoch란, 총 몇번의 학습을 할지에 대한 값 이다. 즉, Epoch가 10 이라면, 같은 데이터 셋으로 10번의 학습을 하게 된다.
Epoch가 많을수록 더 많은 횟수의 학습을 하게 된다. 하지만, 꼭 Epoch가 많을수록 Accuracy가 좋아지지는 않는다. 이는 앞서 ANN에서 말한 오버피팅 등의 이슈가 있기 때문이다.

Batch

Batch란, 한번에 몇개의 데이터를 입력하여 학습을 할지를 정하는 값 이다. Batch사이즈가 커질수록 한번에 많은 데이터에 대한 loss값을 구하고 Gradient disecent에 적용하게 된다. 하지만 많은 메모리를 소모하게 된다. Batch사이즈가 작아질수록, 한번에 적은 데이터에대한 loss값을 구하여 적용하게 된다. 적은 메모리로 동작할수 있지만, 학습속도가 느려지게 된다. 전반적인 경사에 대한 하강이 아닌, 각 데이터에 대한 경사를 구하게 되기 때문이다.

이에 대해 잘 설명해 주신, 앤드류 응 교수님의 강의자료를 첨부한다.(코세라 출처)

여기에서, 파란 경우가 Batch크기가 전체 데이터의 크기와 같은 경우 (:=Batch gradient descent) 초록색이 적정한 Batch Size를 설정한 경우batchsize

score = model.evaluate(data.x_test, data.y_test)
print(score[0])
print(score[1])

10000/10000 [==============================] - 1s 99us/step
0.039372063572064506
0.989

plot_acc(history)

png

plot_loss(history)

png

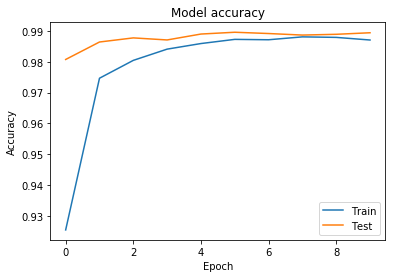
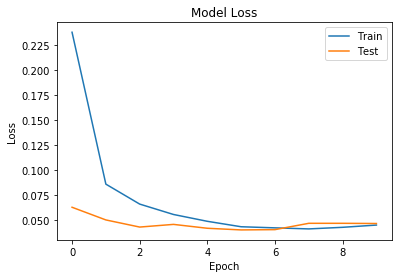
Accuracy가 98.9%까지 올라간것을 확인 가능하다.

칼라 이미지의 경우

from keras import datasets
class DATA():
    def __init__(self):
        num_classes = 10
        (x_train, y_train), (x_test, y_test) = datasets.cifar10.load_data()

        self.X_test = x_test
        self.Y_test = y_test

        img_rows, img_cols, img_ch = x_train.shape[1:]

        if backend.image_data_format() == 'channels_first':
            X_train = x_train.reshape(x_train.shape[0], img_ch, img_rows, img_cols)
            X_test = x_test.reshape(x_test.shape[0], img_ch, img_rows, img_cols)
            input_shape = (img_ch, img_rows, img_cols)
        else:
            X_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, img_ch)
            X_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, img_ch)
            input_shape = (img_rows, img_cols, img_ch)

        X_train = X_train.astype('float32')
        X_test = X_test.astype('float32')

        X_train /= 255.0
        X_test /= 255.0

        Y_train = keras.utils.np_utils.to_categorical(y_train, num_classes)
        Y_test = keras.utils.np_utils.to_categorical(y_test, num_classes)

        self.input_shape = input_shape
        self.num_classes = num_classes
        self.x_train, self.y_train = X_train, Y_train
        self.x_test, self.y_test = X_test, Y_test

모델은 이전의 CNN과 같은 모델을 사용하도록 한다.

batch_size = 128
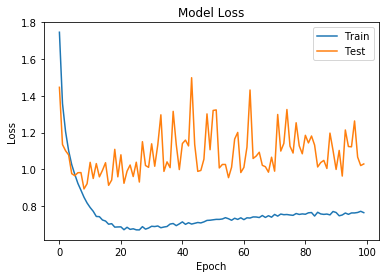
epochs = 100

data = DATA()

model = cnn(data.input_shape, data.num_classes)

history = model.fit(data.x_train, data.y_train, batch_size=batch_size, epochs=epochs, validation_split=0.2)

Train on 40000 samples, validate on 10000 samples
Epoch 1/100
40000/40000 [==============================] - 8s 207us/step - loss: 1.7465 - acc: 0.3748 - val_loss: 1.4466 - val_acc: 0.4833
Epoch 2/100
40000/40000 [==============================] - 8s 195us/step - loss: 1.3579 - acc: 0.5228 - val_loss: 1.1348 - val_acc: 0.6027
Epoch 3/100
40000/40000 [==============================] - 8s 195us/step - loss: 1.2052 - acc: 0.5769 - val_loss: 1.1011 - val_acc: 0.6093
Epoch 4/100
40000/40000 [==============================] - 8s 194us/step - loss: 1.1011 - acc: 0.6121 - val_loss: 1.0780 - val_acc: 0.6271
Epoch 5/100
40000/40000 [==============================] - 8s 195us/step - loss: 1.0255 - acc: 0.6448 - val_loss: 0.9761 - val_acc: 0.6595
Epoch 6/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.9723 - acc: 0.6593 - val_loss: 0.9651 - val_acc: 0.6632
Epoch 7/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.9234 - acc: 0.6816 - val_loss: 0.9813 - val_acc: 0.6668
Epoch 8/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.8860 - acc: 0.6950 - val_loss: 0.9820 - val_acc: 0.6692
Epoch 9/100
40000/40000 [==============================] - 8s 195us/step - loss: 0.8475 - acc: 0.7049 - val_loss: 0.8929 - val_acc: 0.6969
Epoch 10/100
40000/40000 [==============================] - 8s 195us/step - loss: 0.8163 - acc: 0.7200 - val_loss: 0.9214 - val_acc: 0.6926
Epoch 11/100
40000/40000 [==============================] - 8s 196us/step - loss: 0.7917 - acc: 0.7288 - val_loss: 1.0379 - val_acc: 0.6751
Epoch 12/100
40000/40000 [==============================] - 8s 197us/step - loss: 0.7710 - acc: 0.7367 - val_loss: 0.9500 - val_acc: 0.7013
Epoch 13/100
40000/40000 [==============================] - 8s 196us/step - loss: 0.7430 - acc: 0.7461 - val_loss: 1.0310 - val_acc: 0.6688
Epoch 14/100
40000/40000 [==============================] - 8s 202us/step - loss: 0.7419 - acc: 0.7485 - val_loss: 0.9588 - val_acc: 0.6956
Epoch 15/100
40000/40000 [==============================] - 8s 198us/step - loss: 0.7238 - acc: 0.7545 - val_loss: 0.9941 - val_acc: 0.6855
Epoch 16/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.7181 - acc: 0.7566 - val_loss: 1.0358 - val_acc: 0.7018
Epoch 17/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.7007 - acc: 0.7616 - val_loss: 0.9126 - val_acc: 0.7046
Epoch 18/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.7037 - acc: 0.7658 - val_loss: 0.9415 - val_acc: 0.6918
Epoch 19/100
40000/40000 [==============================] - 8s 198us/step - loss: 0.6848 - acc: 0.7723 - val_loss: 1.1086 - val_acc: 0.6637
Epoch 20/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.6858 - acc: 0.7729 - val_loss: 0.9589 - val_acc: 0.6928
Epoch 21/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.6863 - acc: 0.7729 - val_loss: 1.0789 - val_acc: 0.7019
Epoch 22/100
40000/40000 [==============================] - 8s 193us/step - loss: 0.6707 - acc: 0.7785 - val_loss: 0.9237 - val_acc: 0.7102
Epoch 23/100
40000/40000 [==============================] - 8s 193us/step - loss: 0.6840 - acc: 0.7761 - val_loss: 0.9896 - val_acc: 0.7070
Epoch 24/100
40000/40000 [==============================] - 8s 193us/step - loss: 0.6727 - acc: 0.7774 - val_loss: 1.0234 - val_acc: 0.7037
Epoch 25/100
40000/40000 [==============================] - 8s 193us/step - loss: 0.6759 - acc: 0.7778 - val_loss: 0.9605 - val_acc: 0.6997
Epoch 26/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.6701 - acc: 0.7801 - val_loss: 1.0386 - val_acc: 0.6952
Epoch 27/100
40000/40000 [==============================] - 8s 196us/step - loss: 0.6697 - acc: 0.7800 - val_loss: 0.9305 - val_acc: 0.7154
Epoch 28/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.6875 - acc: 0.7785 - val_loss: 1.1503 - val_acc: 0.7034
Epoch 29/100
40000/40000 [==============================] - 8s 196us/step - loss: 0.6738 - acc: 0.7817 - val_loss: 1.0206 - val_acc: 0.7123
Epoch 30/100
40000/40000 [==============================] - 8s 197us/step - loss: 0.6799 - acc: 0.7787 - val_loss: 1.0106 - val_acc: 0.6699
Epoch 31/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.6896 - acc: 0.7762 - val_loss: 1.1388 - val_acc: 0.7105
Epoch 32/100
40000/40000 [==============================] - 8s 196us/step - loss: 0.6880 - acc: 0.7772 - val_loss: 1.0165 - val_acc: 0.7075
Epoch 33/100
40000/40000 [==============================] - 8s 203us/step - loss: 0.6911 - acc: 0.7769 - val_loss: 1.1340 - val_acc: 0.6987
Epoch 34/100
40000/40000 [==============================] - 8s 200us/step - loss: 0.6816 - acc: 0.7797 - val_loss: 1.2967 - val_acc: 0.6981
Epoch 35/100
40000/40000 [==============================] - 8s 197us/step - loss: 0.6855 - acc: 0.7773 - val_loss: 0.9886 - val_acc: 0.7096
Epoch 36/100
40000/40000 [==============================] - 8s 197us/step - loss: 0.6883 - acc: 0.7779 - val_loss: 1.0405 - val_acc: 0.6828
Epoch 37/100
40000/40000 [==============================] - 8s 196us/step - loss: 0.7016 - acc: 0.7758 - val_loss: 1.0090 - val_acc: 0.6871
Epoch 38/100
40000/40000 [==============================] - 8s 208us/step - loss: 0.7045 - acc: 0.7749 - val_loss: 1.3155 - val_acc: 0.7013
Epoch 39/100
40000/40000 [==============================] - 8s 206us/step - loss: 0.6930 - acc: 0.7744 - val_loss: 1.1347 - val_acc: 0.6724
Epoch 40/100
40000/40000 [==============================] - 8s 193us/step - loss: 0.7025 - acc: 0.7741 - val_loss: 0.9985 - val_acc: 0.6704
Epoch 41/100
40000/40000 [==============================] - 8s 193us/step - loss: 0.7134 - acc: 0.7711 - val_loss: 1.1402 - val_acc: 0.7112
Epoch 42/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.7001 - acc: 0.7732 - val_loss: 1.1590 - val_acc: 0.6196
Epoch 43/100
40000/40000 [==============================] - 8s 197us/step - loss: 0.7087 - acc: 0.7736 - val_loss: 1.1273 - val_acc: 0.6945
Epoch 44/100
40000/40000 [==============================] - 8s 197us/step - loss: 0.7016 - acc: 0.7752 - val_loss: 1.4988 - val_acc: 0.7013
Epoch 45/100
40000/40000 [==============================] - 8s 199us/step - loss: 0.7057 - acc: 0.7725 - val_loss: 1.1355 - val_acc: 0.7128
Epoch 46/100
40000/40000 [==============================] - 8s 208us/step - loss: 0.7101 - acc: 0.7722 - val_loss: 0.9887 - val_acc: 0.7001
Epoch 47/100
40000/40000 [==============================] - 8s 200us/step - loss: 0.7078 - acc: 0.7717 - val_loss: 0.9936 - val_acc: 0.6947
Epoch 48/100
40000/40000 [==============================] - 8s 199us/step - loss: 0.7135 - acc: 0.7729 - val_loss: 1.0550 - val_acc: 0.7063
Epoch 49/100
40000/40000 [==============================] - 8s 212us/step - loss: 0.7215 - acc: 0.7696 - val_loss: 1.3017 - val_acc: 0.5829
Epoch 50/100
40000/40000 [==============================] - 8s 205us/step - loss: 0.7225 - acc: 0.7689 - val_loss: 1.1065 - val_acc: 0.6390
Epoch 51/100
40000/40000 [==============================] - 8s 203us/step - loss: 0.7249 - acc: 0.7679 - val_loss: 1.3206 - val_acc: 0.6940
Epoch 52/100
40000/40000 [==============================] - 8s 201us/step - loss: 0.7271 - acc: 0.7661 - val_loss: 1.3234 - val_acc: 0.6998
Epoch 53/100
40000/40000 [==============================] - 8s 197us/step - loss: 0.7270 - acc: 0.7689 - val_loss: 1.0073 - val_acc: 0.7110
Epoch 54/100
40000/40000 [==============================] - 8s 199us/step - loss: 0.7292 - acc: 0.7676 - val_loss: 1.0262 - val_acc: 0.6730
Epoch 55/100
40000/40000 [==============================] - 8s 202us/step - loss: 0.7364 - acc: 0.7664 - val_loss: 1.0263 - val_acc: 0.7111
Epoch 56/100
40000/40000 [==============================] - 10s 243us/step - loss: 0.7305 - acc: 0.7664 - val_loss: 0.9544 - val_acc: 0.7001
Epoch 57/100
40000/40000 [==============================] - 8s 202us/step - loss: 0.7223 - acc: 0.7694 - val_loss: 1.0113 - val_acc: 0.7088
Epoch 58/100
40000/40000 [==============================] - 8s 200us/step - loss: 0.7333 - acc: 0.7665 - val_loss: 1.1647 - val_acc: 0.7039
Epoch 59/100
40000/40000 [==============================] - 8s 199us/step - loss: 0.7269 - acc: 0.7673 - val_loss: 1.2008 - val_acc: 0.7128
Epoch 60/100
40000/40000 [==============================] - 8s 200us/step - loss: 0.7357 - acc: 0.7661 - val_loss: 0.9823 - val_acc: 0.6868
Epoch 61/100
40000/40000 [==============================] - 8s 201us/step - loss: 0.7256 - acc: 0.7673 - val_loss: 1.0100 - val_acc: 0.6758
Epoch 62/100
40000/40000 [==============================] - 10s 258us/step - loss: 0.7356 - acc: 0.7636 - val_loss: 1.1207 - val_acc: 0.7105
Epoch 63/100
40000/40000 [==============================] - 8s 205us/step - loss: 0.7344 - acc: 0.7651 - val_loss: 1.4319 - val_acc: 0.6978
Epoch 64/100
40000/40000 [==============================] - 9s 230us/step - loss: 0.7404 - acc: 0.7657 - val_loss: 1.0589 - val_acc: 0.6942
Epoch 65/100
40000/40000 [==============================] - 37s 928us/step - loss: 0.7401 - acc: 0.7653 - val_loss: 1.0718 - val_acc: 0.7035
Epoch 66/100
40000/40000 [==============================] - 37s 931us/step - loss: 0.7372 - acc: 0.7610 - val_loss: 1.0927 - val_acc: 0.6838
Epoch 67/100
40000/40000 [==============================] - 37s 928us/step - loss: 0.7481 - acc: 0.7606 - val_loss: 1.0217 - val_acc: 0.6777
Epoch 68/100
40000/40000 [==============================] - 37s 917us/step - loss: 0.7376 - acc: 0.7644 - val_loss: 1.0139 - val_acc: 0.6735
Epoch 69/100
40000/40000 [==============================] - 37s 927us/step - loss: 0.7471 - acc: 0.7614 - val_loss: 0.9842 - val_acc: 0.7049
Epoch 70/100
40000/40000 [==============================] - 37s 930us/step - loss: 0.7390 - acc: 0.7617 - val_loss: 1.0657 - val_acc: 0.6596
Epoch 71/100
40000/40000 [==============================] - 37s 928us/step - loss: 0.7540 - acc: 0.7585 - val_loss: 0.9897 - val_acc: 0.6953
Epoch 72/100
40000/40000 [==============================] - 37s 930us/step - loss: 0.7448 - acc: 0.7614 - val_loss: 1.2985 - val_acc: 0.7020
Epoch 73/100
40000/40000 [==============================] - 37s 936us/step - loss: 0.7560 - acc: 0.7587 - val_loss: 1.0992 - val_acc: 0.7130
Epoch 74/100
40000/40000 [==============================] - 37s 933us/step - loss: 0.7526 - acc: 0.7608 - val_loss: 1.1410 - val_acc: 0.7069
Epoch 75/100
40000/40000 [==============================] - 37s 932us/step - loss: 0.7536 - acc: 0.7580 - val_loss: 1.3256 - val_acc: 0.7082
Epoch 76/100
40000/40000 [==============================] - 37s 929us/step - loss: 0.7510 - acc: 0.7595 - val_loss: 1.1258 - val_acc: 0.6267
Epoch 77/100
40000/40000 [==============================] - 37s 932us/step - loss: 0.7492 - acc: 0.7613 - val_loss: 1.0885 - val_acc: 0.6615
Epoch 78/100
40000/40000 [==============================] - 38s 941us/step - loss: 0.7590 - acc: 0.7602 - val_loss: 1.2534 - val_acc: 0.7068
Epoch 79/100
40000/40000 [==============================] - 37s 928us/step - loss: 0.7541 - acc: 0.7594 - val_loss: 1.1280 - val_acc: 0.6349
Epoch 80/100
40000/40000 [==============================] - 9s 235us/step - loss: 0.7569 - acc: 0.7584 - val_loss: 1.0844 - val_acc: 0.6797
Epoch 81/100
40000/40000 [==============================] - 9s 231us/step - loss: 0.7551 - acc: 0.7606 - val_loss: 1.1851 - val_acc: 0.6935
Epoch 82/100
40000/40000 [==============================] - 8s 204us/step - loss: 0.7629 - acc: 0.7586 - val_loss: 1.1437 - val_acc: 0.6973
Epoch 83/100
40000/40000 [==============================] - 8s 200us/step - loss: 0.7643 - acc: 0.7580 - val_loss: 1.1813 - val_acc: 0.7104
Epoch 84/100
40000/40000 [==============================] - 9s 219us/step - loss: 0.7453 - acc: 0.7623 - val_loss: 1.1320 - val_acc: 0.7145
Epoch 85/100
40000/40000 [==============================] - 8s 198us/step - loss: 0.7658 - acc: 0.7582 - val_loss: 1.0126 - val_acc: 0.7004
Epoch 86/100
40000/40000 [==============================] - 8s 199us/step - loss: 0.7567 - acc: 0.7604 - val_loss: 1.0367 - val_acc: 0.7144
Epoch 87/100
40000/40000 [==============================] - 8s 198us/step - loss: 0.7543 - acc: 0.7594 - val_loss: 1.0484 - val_acc: 0.6582
Epoch 88/100
40000/40000 [==============================] - 8s 198us/step - loss: 0.7561 - acc: 0.7599 - val_loss: 1.0045 - val_acc: 0.6941
Epoch 89/100
40000/40000 [==============================] - 9s 220us/step - loss: 0.7516 - acc: 0.7604 - val_loss: 1.1970 - val_acc: 0.7115
Epoch 90/100
40000/40000 [==============================] - 8s 207us/step - loss: 0.7700 - acc: 0.7595 - val_loss: 1.1026 - val_acc: 0.6932
Epoch 91/100
40000/40000 [==============================] - 8s 208us/step - loss: 0.7645 - acc: 0.7556 - val_loss: 0.9993 - val_acc: 0.6877
Epoch 92/100
40000/40000 [==============================] - 8s 208us/step - loss: 0.7466 - acc: 0.7622 - val_loss: 1.1027 - val_acc: 0.6981
Epoch 93/100
40000/40000 [==============================] - 9s 214us/step - loss: 0.7511 - acc: 0.7593 - val_loss: 0.9631 - val_acc: 0.7009
Epoch 94/100
40000/40000 [==============================] - 9s 229us/step - loss: 0.7617 - acc: 0.7578 - val_loss: 1.2141 - val_acc: 0.7017
Epoch 95/100
40000/40000 [==============================] - 8s 209us/step - loss: 0.7546 - acc: 0.7578 - val_loss: 1.1240 - val_acc: 0.7056
Epoch 96/100
40000/40000 [==============================] - 8s 198us/step - loss: 0.7621 - acc: 0.7581 - val_loss: 1.1224 - val_acc: 0.6594
Epoch 97/100
40000/40000 [==============================] - 8s 198us/step - loss: 0.7621 - acc: 0.7594 - val_loss: 1.2632 - val_acc: 0.5719
Epoch 98/100
40000/40000 [==============================] - 8s 201us/step - loss: 0.7646 - acc: 0.7576 - val_loss: 1.0665 - val_acc: 0.7132
Epoch 99/100
40000/40000 [==============================] - 8s 199us/step - loss: 0.7711 - acc: 0.7549 - val_loss: 1.0203 - val_acc: 0.6958
Epoch 100/100
40000/40000 [==============================] - 8s 194us/step - loss: 0.7637 - acc: 0.7603 - val_loss: 1.0291 - val_acc: 0.6656

plot_acc(history)

png

plot_loss(history)

png

score = model.evaluate(data.x_test, data.y_test)
print(score[0])
print(score[1])

10000/10000 [==============================] - 1s 119us/step
1.0261676851272583
0.6636

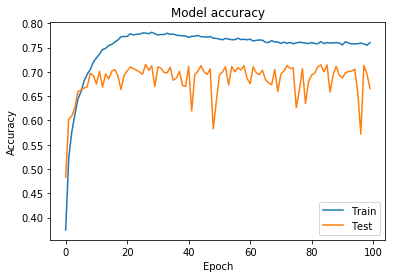
정확도와 loss가 앞선 DNN의 결과에 비해 상당히 좋아진것을 확인 가능함

label= ["airlane",'automobile','bird','cat','deer','dog','frog','horse','ship','truck']

a = 35
plt.imshow(data.X_test[a])
c = model.predict(data.x_test[a:a+1])
print("predict: ",label[c.tolist()[0].index(c.max())])

print("answer: ",label[data.Y_test[a][0]])

predict:  ship
answer:  bird

png

이전에 맞추지 못했던, 35번을 맞췄다고 하고 싶었는데... 똑같이 못맞췄다...

ㅎ... 그래도 아무튼 수치상 성능이 개선되었으므로...

a = 351
plt.imshow(data.X_test[a])
c = model.predict(data.x_test[a:a+1])
print("predict: ",label[c.tolist()[0].index(c.max())])

print("answer: ",label[data.Y_test[a][0]])

predict:  automobile
answer:  automobile

png

A = []
P = []
ANS = []
for a in range(0, 10000):
    c = model.predict(data.x_test[a:a+1])
    pre = c.tolist()[0].index(c.max())
    ans = data.Y_test[a][0]

    if(pre != ans):
        A.append(a)
        P.append(pre)
        ANS.append(ans)
        #print("index: ", a)
        #print("predict: ", pre)
        #print("answer: ", ans)

w = 10
h = 23
fig=plt.figure(figsize=(30, 30))

for j in range(0,230):
    fig.add_subplot(w,h,j+1)
    plt.title(label[P[j]]+":"+label[ANS[j]])
    plt.imshow(data.X_test[A[j]])

png

앞부터 순차적으로 틀린 이미지를 230개 보여주는 코드이다.

DNN에서의 결과에 포함되어있던 많은 결과가 없어진것을 확인 가능하다.

저작자표시 비영리 변경금지

'Study-Machine Learning > Deep Learning' 카테고리의 다른 글

VGG Net 과 CAM (Class Activation Map) 구현  (0) 2018.11.14
VGG Net  (0) 2018.11.08
3.DNN : DeepNeauralNetwork with keras  (0) 2018.07.19
2.simple ANN with Keras  (0) 2018.07.18
혼자 해보는 Pytorch 튜토리얼 -2.1- (0.4.0 수정)Windows에 Pytorch 설치하기  (0) 2018.05.01

댓글()
이전 1 2 3 4 5 6 ··· 13 다음

티스토리툴바